
数学なんていまさら必要なし。加算乗除ができれば生活に支障はないと思っている人は多いだろう。歌の文句にもあるけれど、「サイン・コサイン何になる!」なのだ。
「いやいや、ちょっと待った!」と一声を発したのが数理学博士の近藤宏樹さん。
数学は毎日の暮らしの中にあふれている
近藤さんは幼少期から数学が好きで、高校生のときには国際数学オリンピックに日本代表として出場し、3年連続してメダリストになった数学脳の持ち主。
数学が苦手な側からすると、なんで数学が好きなのか不思議でならないが、
「特別な教育を受けたわけではなく、ただ小学生のときに公文式の塾に通っていて、計算は得意でした」
それが長じて、東大では数学科で学んだという数学大好き人間になったそうだ。
「毎日の暮らしの中に数学はあふれています。例えば、新型コロナウイルスの陽性者数が毎日発表されていて一喜一憂していますが、患者数だけをとらえるのではなく、陽性率などの数字を多面的にとらえていくことが必要なんです。コロナだけではありません、もっと身近なところでは、スーパーに買い物に行けば、物の値段や、ポイント加算で計算力が必要になります。天気予報だって数学が関係しています」
というわけで、天気予報で発表される降水確率ってどういう意味なのか、宝くじって本当に当たるのか、自分はあと何年くらい生きられるのか、電子レンジのワット数についてなど、学校の数学では習わない、生活に役立つ数学の知恵を近藤さんが教えてくれます。
「少しでも数学っておもしろいと思ってもらえたらうれしいですね」
◎降水確率30%のとき、雨は降るの? 降らないの?
天気予報でよく耳にする降水確率。「例えば降水確率30%とは、同じ気象状況が何回もあったとしたら、そのうち雨の降る日の割合が約30%あるということです」。つまり10回に3回の割合で雨が降るということ。
次に降水確率30%のときに、洗濯物は取り込むべきか、それとも干しっ放しで出かけていいのかを考えてみよう。
まず取り込むのに20分、雨に濡れてしまって洗い直すのに60分を要すると仮定。毎回取り込んでいれば、雨が降っても降らなくても1回にかかる時間は20分。干しっ放しにしておくと、10回に3回は雨が降って洗い直すことになり、1回にかかる平均時間は18分(写真ページの表を参照)。
つまり、毎回取り込むよりも、取り込まないほうが効率はよいということになる。
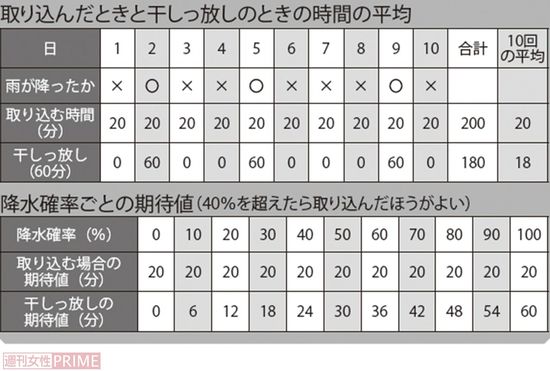
「このように長い目で見たときの平均的な値を、期待値と呼びます。期待値を使って天気を判断すれば、家事も合理的にこなせそうですね」
降水確率が他の数値の場合はどうなのかは、同じく写真ページの表を参照してほしい。この結果から、40%以上になったら、洗濯物は取り込んで出かけたほうがよさそうだ。
300円の宝くじの期待値は150円!?
◎億万長者になりたいけれど、宝くじは当たる? 当たらない?
降水確率で覚えた期待値で、宝くじについて考えてみよう。
第731回年末ジャンボ宝くじの本数は5億本。1等は7億円で当せん確率は0・000005%、最下位当せんの7等が300円で当せん確率は10%。当せん金のすべてと確率を計算して期待値を割り出すと、当せん金の期待値は150円。
長い間買い続けていれば、300円で購入した宝くじからは150円の当せん金が戻り、半額の150円分は損失になる。
「極端な話、売り出された5億本の宝くじを全部買っても、購入金額の半額しか戻ってこないということですよ」
やっぱり宝くじは損する?
「期待値は長い目で見たときの平均的な値。現実的には全部買い占めるなんてこともできませんから、期待値のとおりになるかはわかりません。期待値では損という結果が出ても、1回試して大当たりということは否定できません」
数学的には損するようにできているけれど、もしかしたら大当たりもあるってことだ。損は承知で、やっぱり夢を買ってみますか。
◎自分の手を使って、来年の今日は何曜日かを割り出す
「お母さんの誕生日は何曜日だっけ」なんていうときのように、曜日を知りたくなったとき、指を見るだけでわかるというのが、曜日計算術。
(1)まずは月の位置を覚えよう(毎年変わらない)
指の関節に1から12までを振り分け(左右どちらの手のひらでもOK)、位置を覚える。この番号が1月1日、2月1日……12月1日の曜日になっている。
(2)曜日の位置を覚える(毎年変わる)
写真ページの図に示した曜日は、2021年の曜日の位置。1月1日は人さし指のいちばん上で金曜日、2日はその下で土曜日と続いていく。2月1日は中指のいちばん上で月曜日、2日は火曜日となる。

ちなみに2022年は、曜日を1つずらして人さし指のいちばん上が土曜日になる。
「カレンダーも見ずに、何月何日は月曜日ですよ~と簡単に答えられるので、みんなから驚かれるかもしれませんね(笑)」
自分の余命を詳しく知りたいなら
◎平均寿命はあてにならない!?
よく勘違いされているのが、平均寿命と平均余命。令和元年に発表された女性の平均寿命は87・45歳。このときの平均寿命とは、令和元年に生まれた子どもが平均で何年生きられるかなのだ。
では自分はあと何年くらい生きられるかを知るには何を見ればいいのか。もちろん、年齢だけでなく現在の健康状態にもよるが、自分と同じ年齢の人たちが、あと何年生きられるのかは厚生労働省が発表している平均余命(写真ページ参照)でわかる。
0歳では平均寿命=平均余生なのだが、例えば、40歳女性が平均して何歳まで生きられるかは、現在の年齢40歳+余命48・11歳=88・11歳となり、この年齢までは生きられると、おおよその見当がつけられる。
◎スーパーでたくさんの荷物を同じ重さに振り分ける方法
スーパーで買い物をして、2つの袋に同じくらいの重さに分けるには、さてどうしたらいいのか。
「これは数学でいう組み合わせ術。荷物を重い順に並べ、重いほうから順番に交互に袋に入れていく。その際、入れるときは軽いほうの袋に入れるのがコツですよ」
こんな簡単な方法で、ぴったり同じ重さにならないまでも、少ない誤差でバランスよく振り分けることができるのだ。
数学のこんな知恵、知っていると本当に役に立つ。
◎頭の中でササッと足し算、引き算ができるようになる
暗算は得意だろうか。2ケタくらいはできるにしても3ケタ以上だと難しいが、スーパーで買い物しながら、いくらくらいかかるか足し算ができる。あるいは支払いのとき、いくら払えば、お釣りの小銭を少なくできるか引き算ができる。主婦ならこのくらいはササッとできるようになりたい。
●お釣りの計算が得意になる引き算とは
1000-658の計算をやってみよう。繰り下がりが多くて、頭の中で計算するのはかなり面倒なのだが、引き算の速算には、各ケタの9から引いて、最後に一の位にだけ1を+という方法がある(写真ページの図1)。
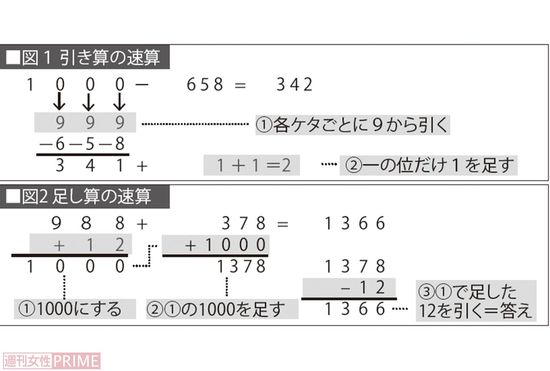
この計算式は1000=999+1と考えるところがポイント。10000から引く場合も、10000=9999+1と考えればよいわけだ。
「引き算が素早くできれば、お釣りの小銭を増やさないようにすることもできるでしょう」
●買い物金額がすぐに計算できる足し算とは
足し算の速算に挑戦してみよう。988+378の計算では、繰り上がりの計算をするよりも、988に12を足すと1000になることを利用したほうが簡単だ。(同・図2)
「速算の計算法はいくつもありますが、基本的な2例です。ぜひマスターしてください」
レンチン時間の割り出し方も解説
◎500Wのレンジで3分のとき、600Wだと何分になるの?
冷凍食品に記載されている電子レンジの加熱時間の目安。でも家にあるレンジはそのワット数が対応していなかったら、どうする。
数学的に難しく言うと、ワット数と加熱時間は反比例の関係にあるということになる。
これを近藤さんに計算してもらったのが下表の対応時間。
500W3分の目安の冷凍食品を600Wでチンするときは、1分について10秒縮めることになる。
「計算では、ワット数に応じて時間を変えねばなりませんが、それは面倒ですよね。そこで
おおよその目安として、1分強につき20秒と考えて、セットするとよいでしょう」
でも、「確かに概算ですが、料理に影響が出ない許容範囲内であると考え、これも数学的な考え方なんですよ」
・500Wの時間を600Wにする→1分につき10秒縮める
・500Wの時間を700Wにする→1分10秒につき20秒縮める
・500Wの時間を1000Wにする→目安時間のおおよそ半分
*逆の場合は目安時間を増やす。
《「女性は数学が苦手」って本当?》
脳の構造の違いから、女性は言語機能に長けていて、男性は抽象的に思考することが得意なことから数学に強い、という説がある。しかし最近の学説では脳には男女差はないという研究発表も出ている。
また近藤さんも、「高校生に数学を教えていますが、数学が得意な女生徒もいます。ただ女性は、自分は数学が苦手なんだと思い込んでいる傾向があります。その背景には、男女の役割期待の違いで、女性に数学を求めなかったこともあるのかもしれません。先入観にとらわれず、数学的センスを磨いてほしいですね」と数学女子に期待。すっかり頭が固くなってしまった中高年女性はどうしたらいいのが、「脳トレによいと計算ドリルが人気ですが、ドリルだけでなく実践でも頭を鍛えてください」
《大ざっぱに把握するのも数学的知恵》
多くの人は「数学の答えはただひとつ」だと考えている。数学の好きな理由に答えがはっきりと決まることがわかりやすくていいともいう。「しかし、答えははっきりと出さないという手法も数学にはありなんです」と近藤さん。
例えば、レンチンのワット数は正確でなくてもこのくらいという見当がつけば問題はない。ここで大切なのは、このくらいの範囲をどのくらいにするか。適当でいいと長時間かけていれば、食品は食べられなくなってしまう。おいしく食べられる範囲内で、おおよその見当をつけるのも数学の知恵だ。また降水確率や宝くじの当せん確率も、期待値という数字で表すことで、絶対ではないけれど、こう考えられるという方向性は見えてきます。
数学の知恵をもっと気楽に生活に活用していきたいもの!
〈取材・文/水口陽子(つきぐみ)〉
【PROFILE】
近藤宏樹さん ◎東大卒の数理学博士。東京大学理学部数学科卒業、同大学院修士課程修了。博士(九州大学数理学)。現在は数学教員、また国際数学オリンピック日本委員会副委員長を務める。

